본인 풀이 (7/1)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t;
ll n;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin >> t;

    for (int i = 0; i < t; i++){
        cin >> n;
        int cnt2 = 0;
        int cnt5 = 0;

        for (int j = 1; j <= n; j++){
            int k = j;
            while (k % 2 == 0)
            {
                cnt2++;
                k /= 2;
            }
            while(k % 5 == 0){
                cnt5++;
                k /= 5;
            }
        }
        if(cnt2 > cnt5){
            cout << cnt5 << "\n";
        }else{
            cout << cnt2 << "\n";
        }
    }
    return 0;
}

1. 로직 생각해내기가 어려워서 강의를 통해 힌트 얻고 시작
2. 1~n까지 순회하며 각 숫자 내에 2와 5가 곱해진 숫자들을 구함
3. 그 중에 더 작은 개수를 가진 수만큼 10이라는 숫자가 만들어짐
4. 총합을 구한 뒤 출력
5. 위의 로직은 시간초과 발생(10억에 대한 숫자를 순회해야하는 경우때문)

모범 답안

선형적으로 순회하는 방식의 로직으로는 풀이 불가능함. 우선 10의 개수는 팩토리얼 연산결과에서 2와 5의 각 제곱수 중 더 작은 개수로 만들어진다.

1, 2, ... n 각 수에 포함된 2의 갯수는 n보다 작은 2의 제곱수 배수의 합이다.

2^k * p < n인 상태에서 k=1,2,...이고, 이때 p의 총 합을 구하면 된다. p는 n에서 2^k를 나눠주면 된다. (몫 연산)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t;
ll n;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin >> t;

    for (int i = 0; i < t; i++){
        cin >> n;
        int cnt2 = 0;
        int cnt5 = 0;

        for (int j = 2; j <= n; j *= 2){
            cnt2 += n / j;
        }
        for (int j = 5; j <= n; j*=5){
            cnt5 += n / j;
        }
        cout << min(cnt2, cnt5) << "\n";
    }
    return 0;
}

복습 (7/17)

코드 로직에 대한 이해가 어려웠는데, 시각화를 다시 해보니 이해가 어렵지 않았다.

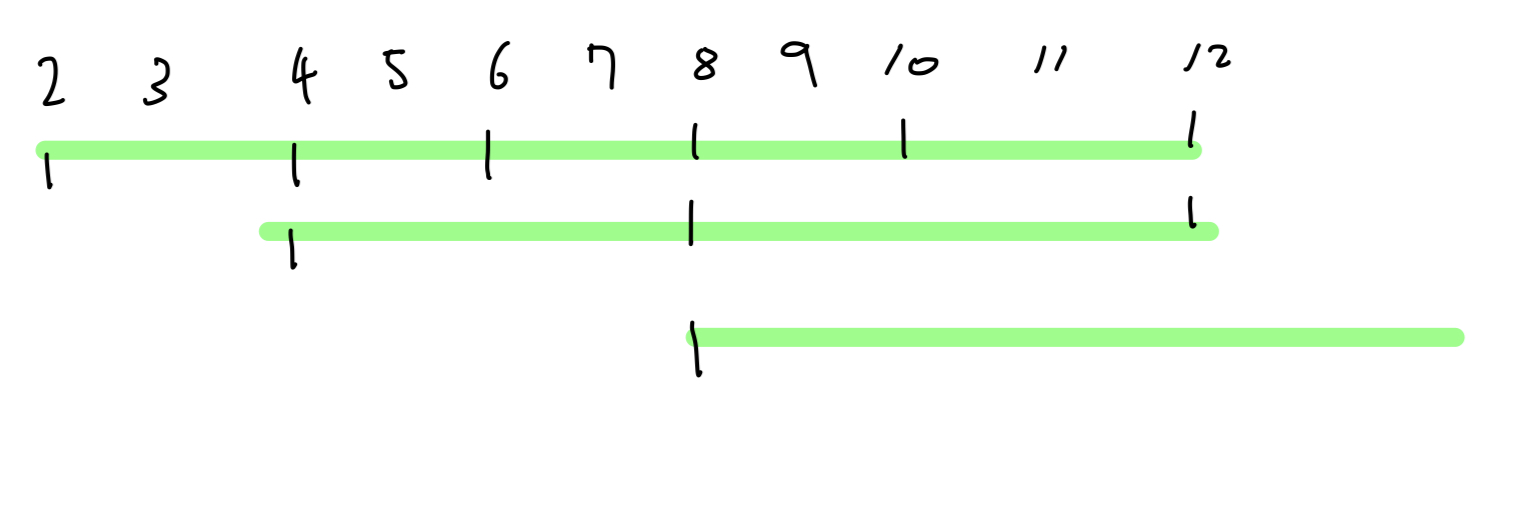
제곱에 대한 계산 필요없이 2의 배수, 2의 2제곱의 배수, 2의 3제곱의 배수, (4의 배수, 8의 배수) 각각 약수 갯수를 계산하여 더해주면 팩토리얼 값 내에 포함된 모든 2의 갯수가 구해진다.

5의 갯수역시 동일하게 구한다.