# 그래프 위상 정렬
# DAG
DAG는 사이클이 없는 방향 그래프를 의미한다.
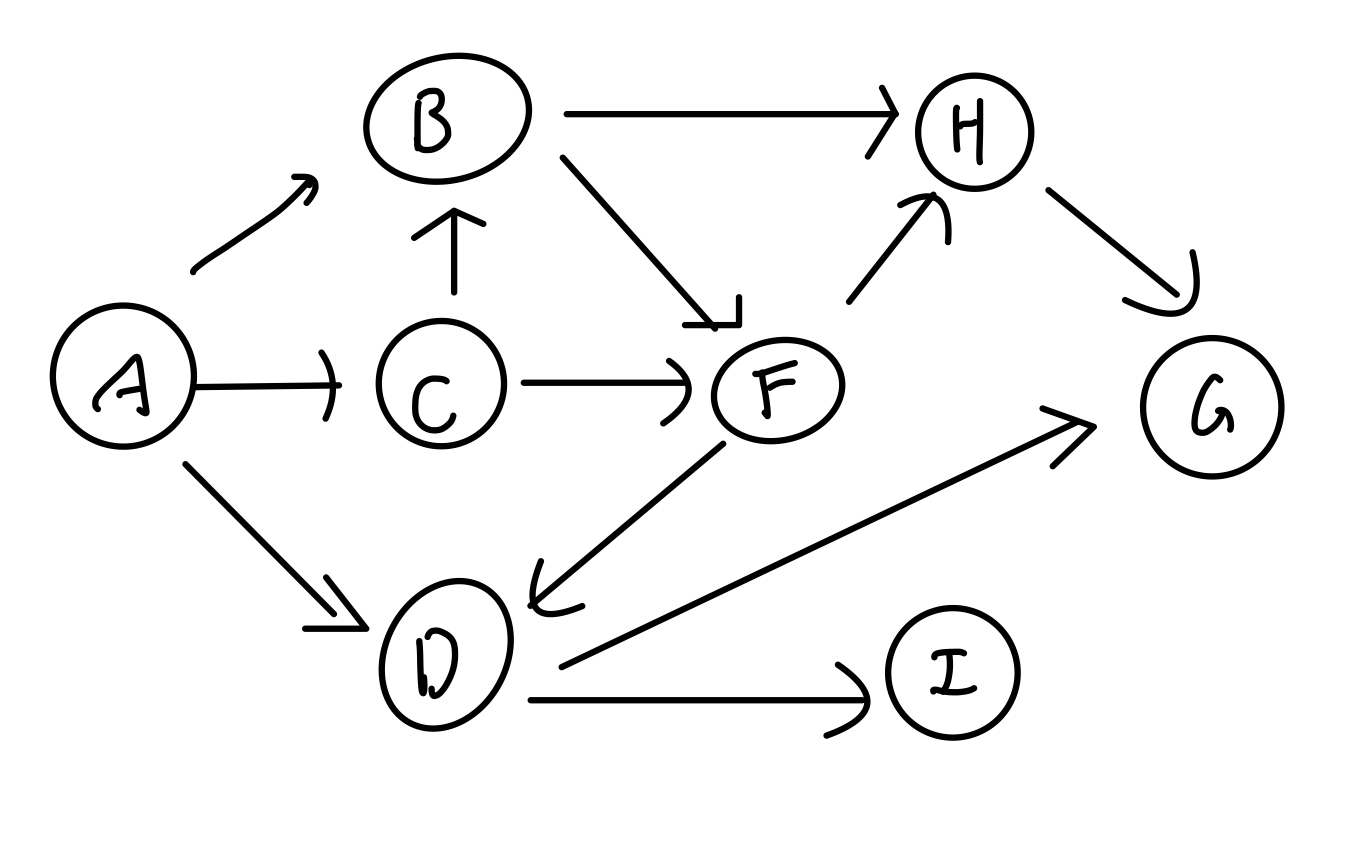
위 DAG 그래프를 차례로 순회할때 정렬되는 노드를 표현하면
A
|-- C --|
| |-- B -- F-- D -- I -- G
| |-- H (H 먼저 완료 후)
DAG 순회의 가장 중심이 될 규칙은 자신을 가리키는 노드들이 모두 인접한 노드의 순회를 끝마친 상태여야 한다는 것이다.
규칙에 따라 DAG를 순회하다 보면 동일한 위상을 갖는 H,D 노드를 볼 수 있는데, 이로 인해 DAG 순회의 결과 노드집합은 여러 경우를 가질 수 있다.
(A -> C -> B -> F -> D -> H -> I -> G)
(A -> C -> B -> F -> H -> D -> I -> G)
이러한 정렬 방법을 위상 정렬(topological sorting) 이라고 한다.
DFS 기반으로 pre/post 변수를 통해 그래프 순회를 하고 post값이 내림차순으로 정렬 되도록 노드를 나열하면 된다.
# Weighted DAG
가중치가 있는 DAG에서 최장경로를 구하는 문제가 있다. DAG 순회 방식을 채택한 뒤, 정점 v에서 w까지 가는 동안 각 인접 노드를 순회할 때 가중치가 가장 크게 잡히는 경로부터 순회하면 된다.
algorithm findLongestPath(인접 리스트, 노드 수 n, 정점 w, 정점 t, 최장경로 저장 배열 arr){
정점 w = "visited"
if(정점 w == 정점 t){
return 최장 경로 길이는 0
}
while(노드의 인접리스트가 없을 때까지){
정점 v 선언, v = w로 초기화 (w부터 인접한 노드들을 재귀적으로 v를 통해 순회할 예정)
if(v is not visited){
# 재귀호출, w -> v까지 가는 동안의 최장경로
findLongestPath(인접 리스트, n, v, t, 최장경로 저장 배열 arr)
# 현재 노드인 w까지의 최장경로와 w에서 v까지의 최장 경로 길이를 비교
arr[w] = max(arr[w], arr[v] + v.weight)
} else { // w 인접노드인 v가 방문노드
# v가 이미 방문한 노드이므로 해당 노드까지의 최장경로 비용이 저장되어 있음
arr[w] = max(arr[w], arr[v] + v.weight)
}
v = w의 또 다른 인접노드
}
}
Weighted DAG의 최종 수행시간은 O(n+m)이 된다.
# Bellman Ford 알고리즘
Bellman Ford 알고리즘은 그래프 최단 경로 알고리즘 중 하나이다.
아래 그래프를 고려하자.
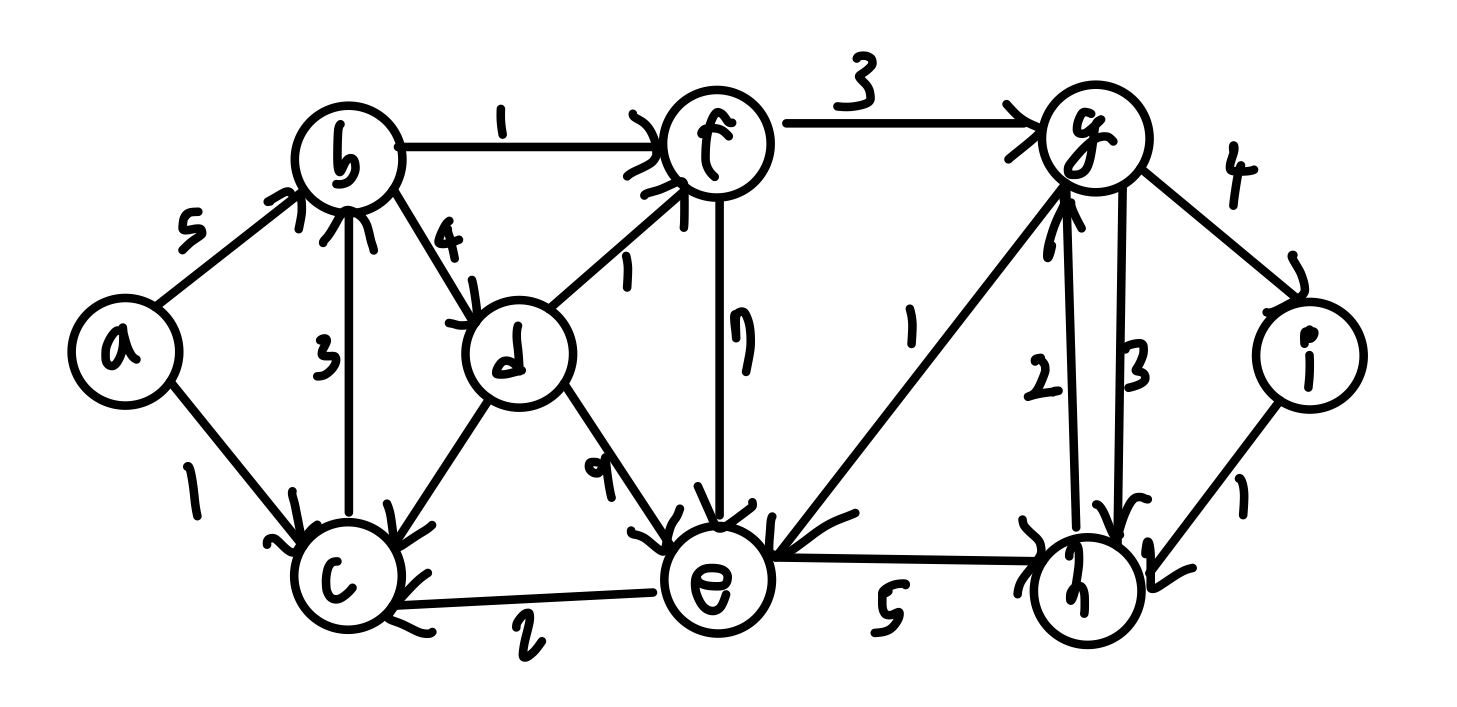
단순 노드의 개수로 최단 경로를 구하면
(a -> b -> f -> g -> i) 또는
(a -> c -> e -> h -> u) 가 된다.
하지만 각 엣지마다 가중치가 부여되어 있기 때문에 이를 고려하여 최단 경로를 구하면
(a -> c -> b -> f -> g -> i) 로 길이가 12가 된다.
이를 재귀적으로 생각하면 (a->i) 로 가는 최단 경로는 (a -> g) 까지의 최단 경로 + (g->i) 까지의 엣지 가중치 값이다.
이를 정리하여 dist[v] = s(source)에서 v로 가는 최단 경로의 길이 로 정의할 수 있다.
또한 목적지 v에 인접하면서 v를 가리키는 노드들이 존재한다면
dist[v] = min(dist[u1] + w(u1,v), dist[u2] + w(u2, v), dist[u3] + w(u3, v)) 로 정의할 수 있다.
또한, 최종적으로 u1, u2, u3 등 목적지 직전 인접 노드까지 최단경로를 모두 계산한 값이 목적지 노드에서의 계산된 최단 경로의 길이보다 작다면 이를 인접 노드까지의 최단 경로 값으로 새롭게 초기화한다. 이를 릴랙스 relax(u, v) 라고 표현한다.
if dist[v] > dist[u] + w(u, v):
dist[v] = dist[u] + w(u, v) # relax!!
초기에 각 노드의 계산된 최단 경로 길이값을 math.inf로 초기화한 뒤에 최단경로를 계산하며 각각 릴랙스처리 해주면 된다.
다음은 위 최단경로 알고리즘의 예시이다.
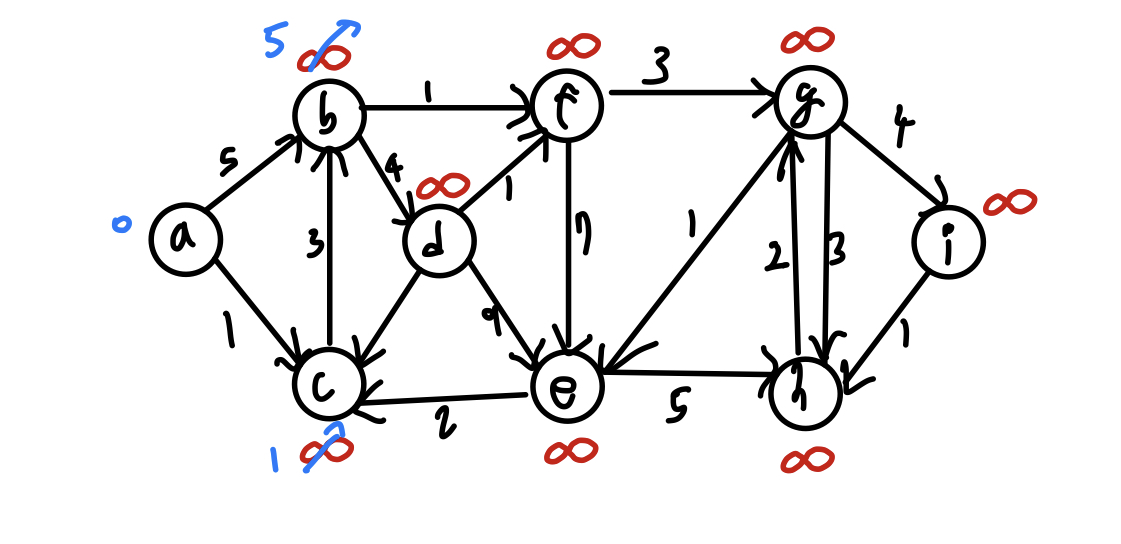
노드 b와 노드 c가 각각 5, 1값으로 초기화 되었다.
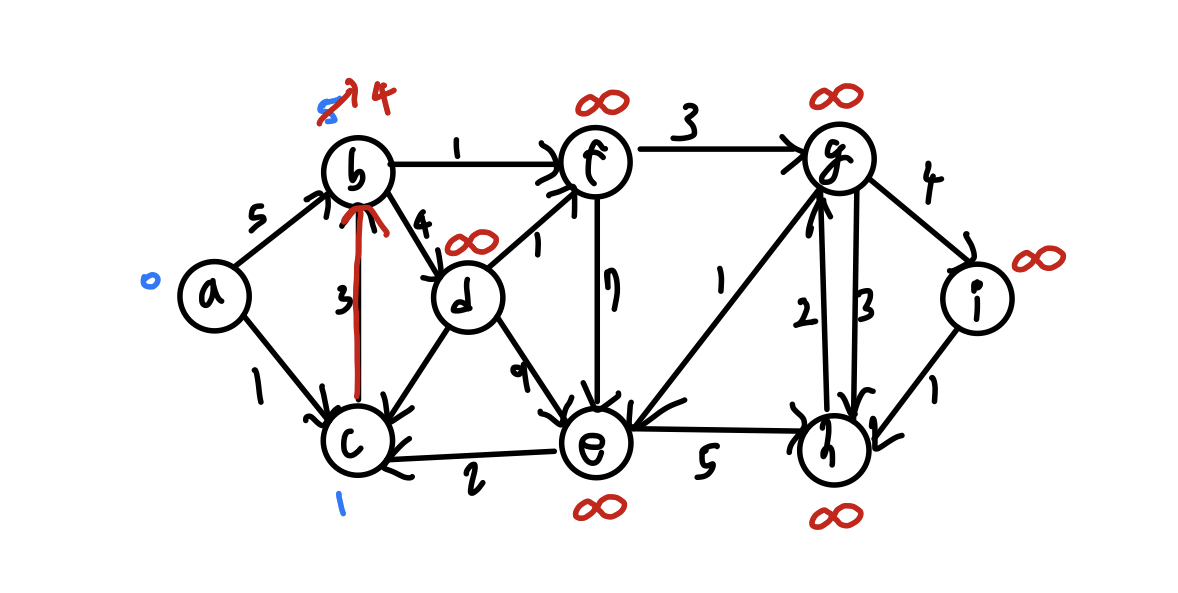
(a -> c -> b) 경로의 가중치 계산 값에 따라 현재 b가 갖는 가중치 값인 5보다 (a -> c -> b) 경로의 가중치 값이 더 작으므로 4라는 값으로 새롭게 초기화 된다.
최단경로를 계산하기 위해 거치는 노드는 소스 노드(Source)와 목적지 노드 (V)를 제외하여 총 n-2 개를 넘지 않는다.
TIP
가령 소스노드 S로부터 목적지 노드 V까지의 최단 경로를 계산하는 상황을 고려해보자. S부터 V까지 전체 노드의 개수는 n개일 때
S를 제외한 n-1개의 노드가 릴랙스 되어야 하므로 n-1 라운드를 마련하여 루프를 돌린다.
최단경로 계산이 되지 않은 무작위 노드들은 math.inf 끼리 연산이 되므로 릴랙스에 의미가 없다.
또한 각 라운드마다 모든 엣지에 대해 릴랙스 해주어야 한다. 이를 n-1 라운드 동안 진행한다.
for i in range(n-1): # n-1 round
for each edge(u, v) in G:
if dist[v] > dist[u] + w(u,v):
dist[v] = dist[u] + w(u,v) # relax(u, v)
위의 이중루프가 Bellman-Ford 알고리즘 이며, 총 수행시간은 O(n X E) (E는 전체 엣지 수)이고 엣지는 최대 n의 제곱만큼 생성될 수 있으므로
O(n³)이 된다.
# Dijkstra 알고리즘

위의 벨만 포드 알고리즘은 수행시간이 너무 느리다. 이에 비해 더 빠른 다익스트라(Dijkstra) 알고리즘 을 알아본다.
먼저 슈도 코드를 살펴보면
Q = min_heap with dist[v] # 최소 힙
while Q != ∅ : # 힙에 원소가 없을 때까지
u = Q.deleteMin()
for each u->v: # u에 인접한 모든 노드들에 대해
relax(u, v)
Q.decreaseKey(v, dist[v]) # heapify Up - O(logn)
위 알고리즘에 따라 노드를 순회하면
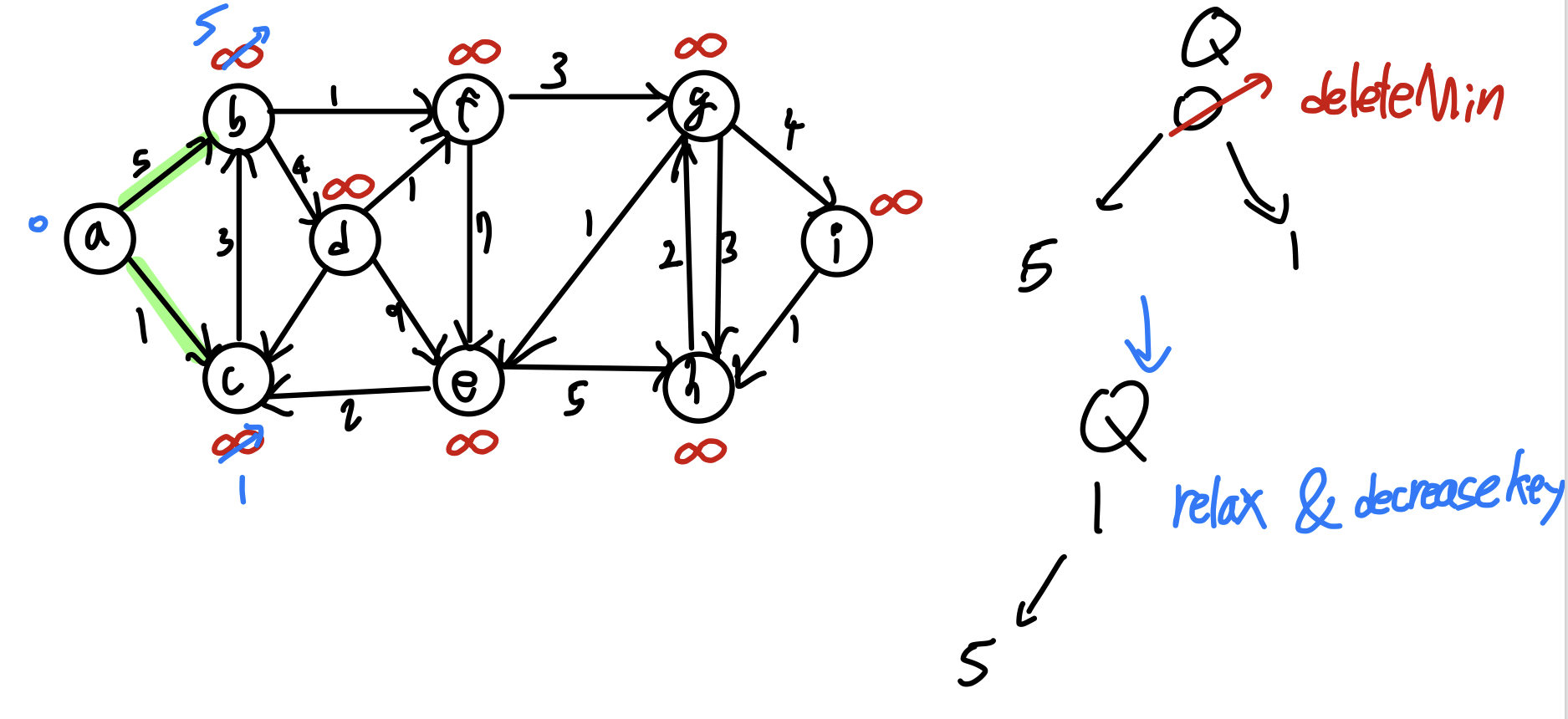
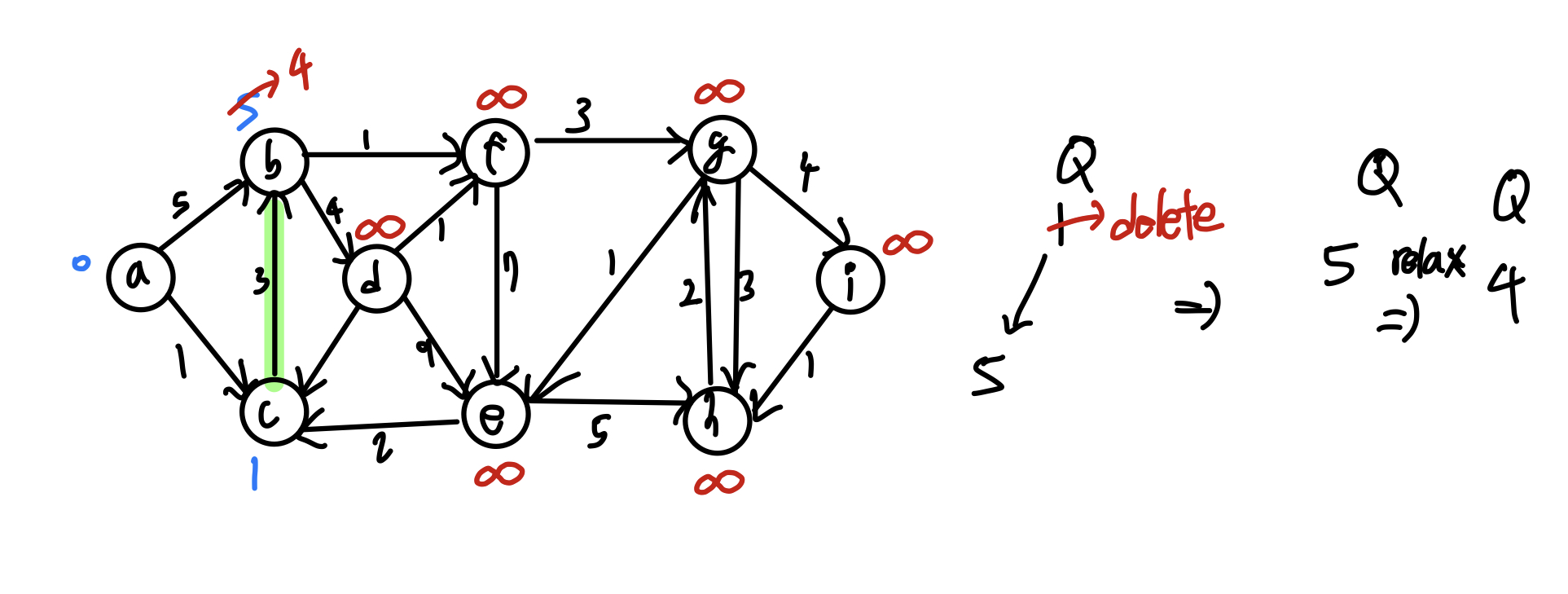
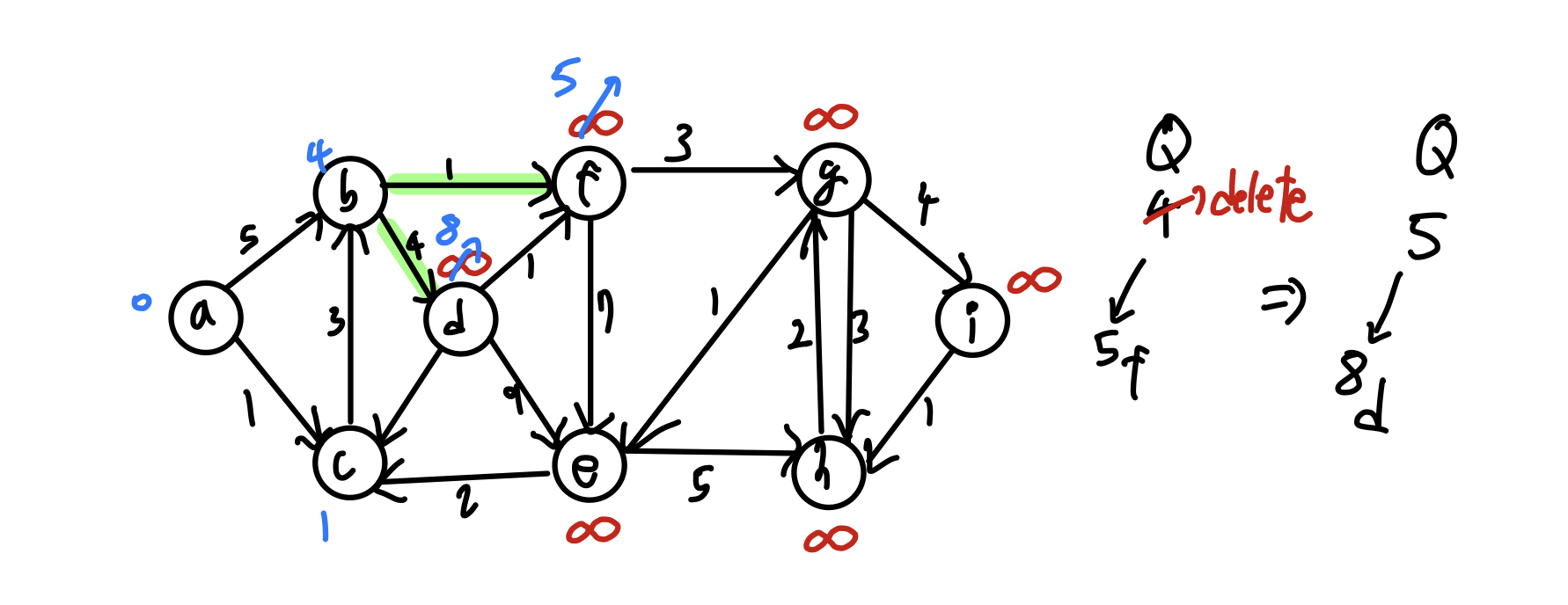
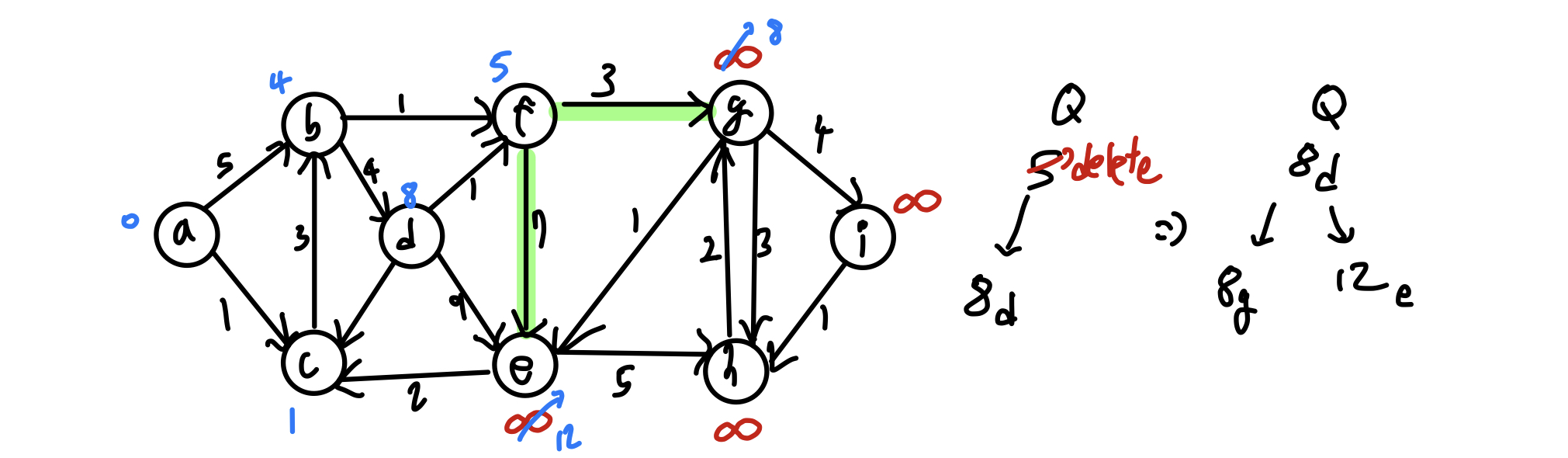

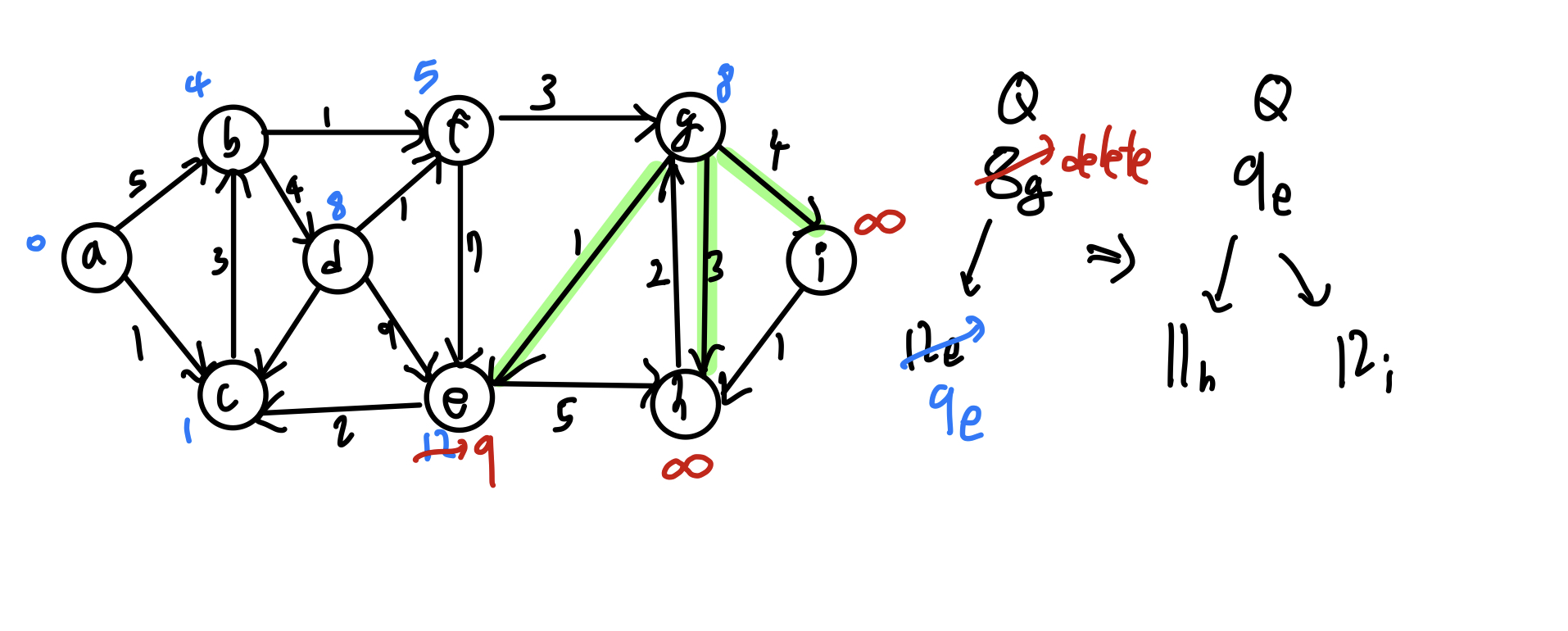
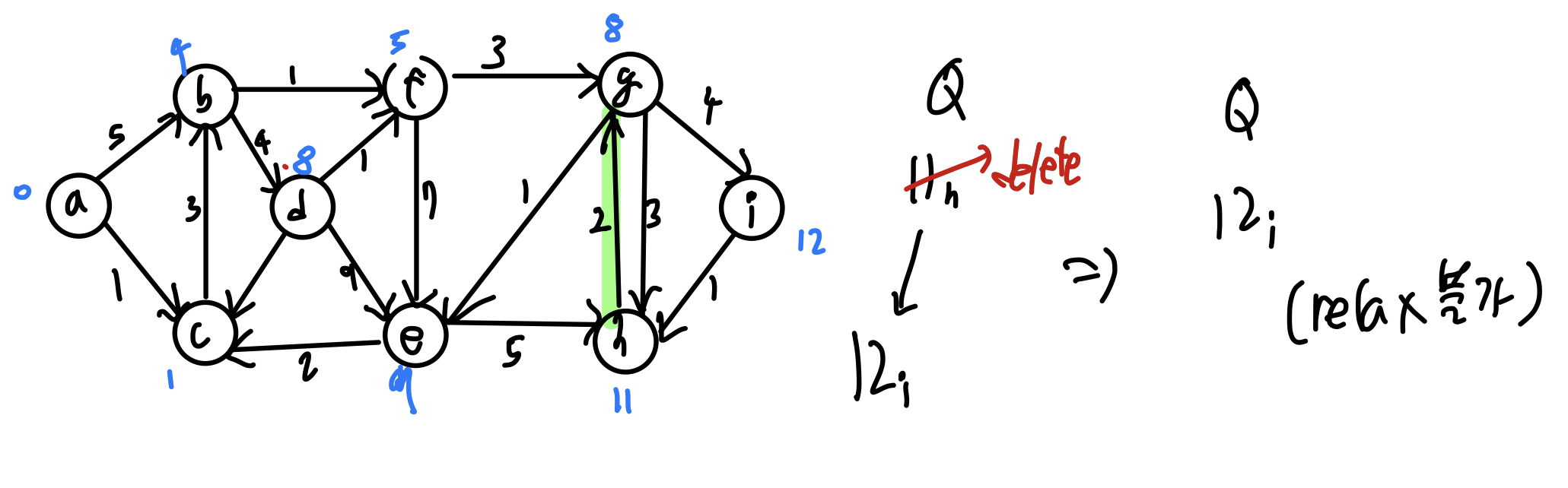
최소 힙 자료구조는 다음을 참조한다. (opens new window)
수행시간의 경우 각 노드가 모두 최소 힙에 한 번의 삽입과 한 번의 삭제가 이루어지므로 O(nlogn) 시간이 소요되고
각 에지가 모두 릴랙스 후 heapify up연산을 진행하므로 O(E x logn) = O(n²logn) 시간이 소요된다.
따라서 총 소요시간은 O(n²logn) 가 된다.
# Dijkstra 구현 코드
s = 0 # s is source node
dist = [0,∞,∞,.....,∞,∞]
parent = [None, None,.......,None] # parent를 통해 최단경로를 구성한다!
min_heap Q = all nodes v with key dist[v]
while Q is not empty:
u = Q.deleteMin()
for each edge u->v:
relax(u,v) # relax 하면서 parent에 데이터를 추가한다.
Q.decreaseKey(v, dist[v]) in Q
return dist, parent
parent 리스트가 바로 그래프 무작위 노드에서 노드로의 최단경로를 표현해둔 데이터이다.