동적계획법을 사용하는 이유

알고리즘 풀이를 분할정복 관점으로 접근할 때 관점은 두 가지가 존재한다.

1. 일반적인 재귀적 풀이로 접근할 것인가
2. 동적계획법 풀이로 접근할 것인가

같은 분할정복이어도 수행시간과 메모리 측면에서 동적계획법이 우월한 경우가 많다.

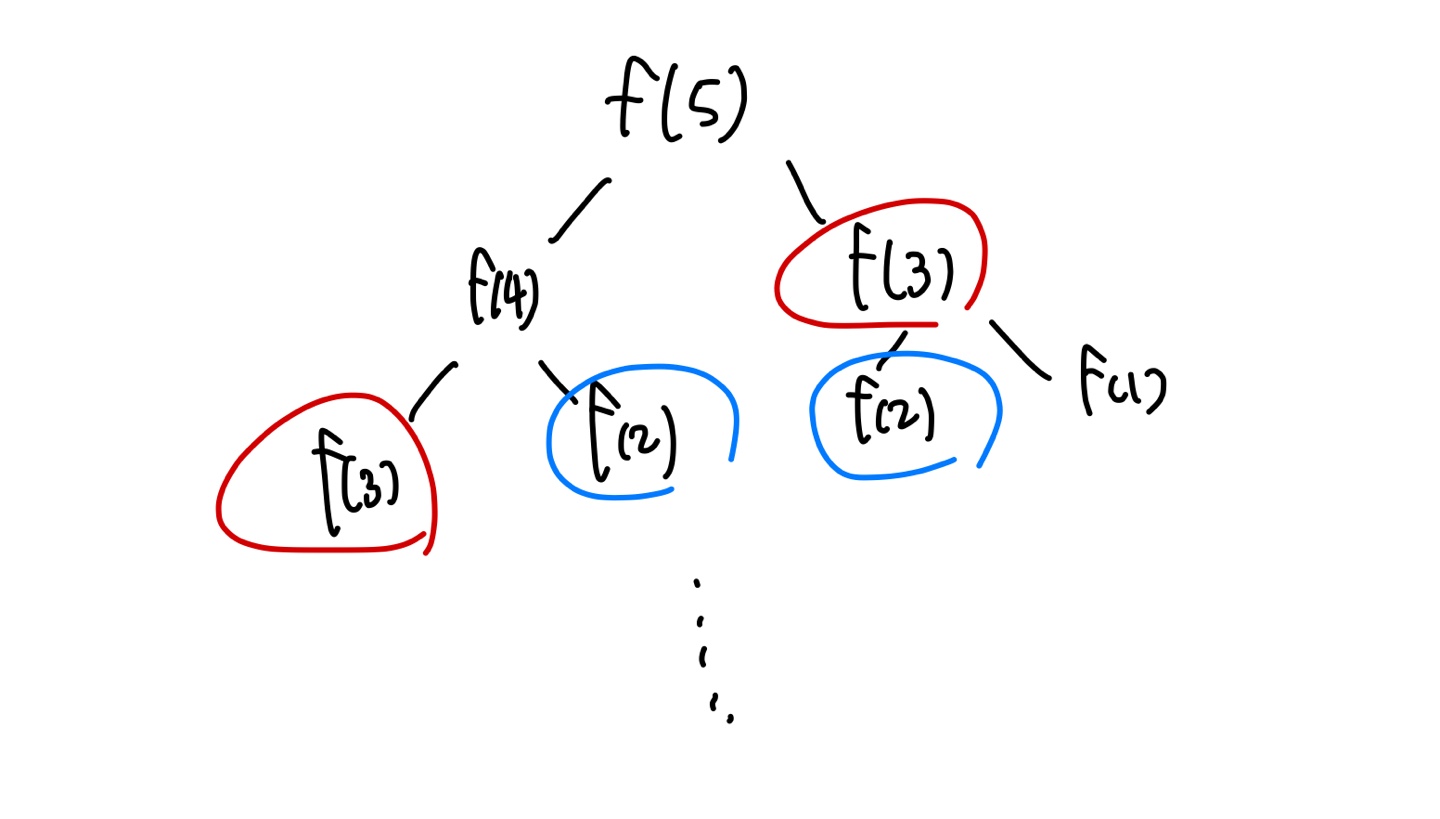
이는 재귀적으로 호출한 경우인데 f(3)과 f(2)가 중복되게 호출되는 문제를 확인할 수 있다.

재귀호출의 문제점 해결을 위해 동적계획법을 활용하면 다음과 같다.

def dp(n):
    F = [0,1]
    for i in range(2, n+1):
        F.append(F[i-1] + F[i-2])
    return F

a = dp(3)
print(a[-1])

재귀호출과 가장 큰 차이점은 데이터를 테이블에 저장하는가이다. 동적계획법의 테이블은 필요한 데이터를 상수시간에 출력할 수 있다는 것이 가장 큰 장점이다.

TIP

Time complexity of recursive Fibonacci Program (opens new window)에 따르면
재귀호출 피보나치 수열의 시간복잡도는 약 O(1.6^n)이고

동적계획법 피보나치 수열의 시간복잡도는 약 O(n)시간이다.

DP 예제 1 - 계단오르기

계단은 1칸 또는 2칸씩만 오를 수 있다. 1층부터 n층까지 오르는 데에 발생하는 경우의 수는?

DP도 분할정복이라는 알고리즘 해결방법이 기본적으로 깔려있기 때문에 바닥조건설정이 가장 우선시 된다.

바닥조건은 A[1]=1, A[2]=1이며 1층에 있을 때와 2층으로 오르는 경우의 수가 바닥조건이 된다. (2층으로 오르는 데에는 계단 한칸만 필요하므로 A[2]=1이 된다.)

이를 바탕으로 점화식을 세우면 A[n] = A[n-1] + A[n-2]가 된다.
(n층까지 오르는 경우의 수는 n-1층까지의 경우의 수 + n-2까지의 경우의 수)

피보나치 수열과 같은 알고리즘이므로 코드 구현은 위를 참조