# Graph 자료구조
통상 G = (V, E)로 표현하며 V는 정점(Vertex) E는 (Edge set)을 의미한다. 엣지는 링크로도 불린다.
# 그래프 용어
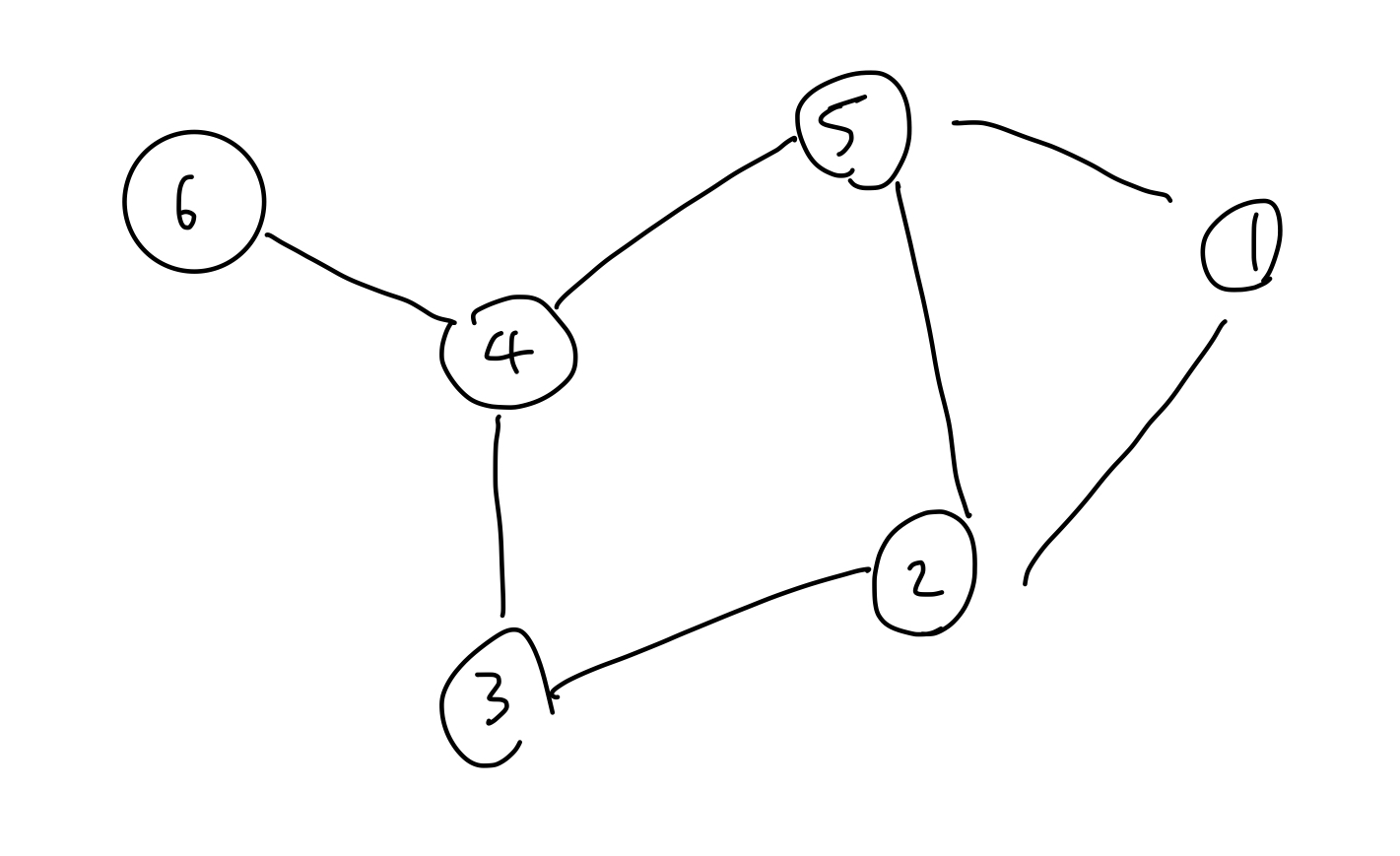
- 각 동그라미 -> Vertex, 정점이라고 한다. 또는 노드라고도 불린다.
- 각 정점을 잇는 선분을 엣지(Edge), 혹은 간선이라고 한다.
- 분지수 (degree) -> 특정 노드에서 뻗어져 나갈 수 있는 엣지의 수. 4의 분지수는 3
- 인접하다 (adjacent) -> 에지 (4,5)에서 노드 (4), 노드 (5)는 인접하다.
- 인접하다 (incident) -> 에지 (4,5)는 노드 (4), 노드(5)와 인접하다.
- 경로(path) : 3-2-5 특정 노드에서 특정 노드까지 가는 동안 거치는 노드들 (단 지나가는 동안 중복되는 노드는 존재하면 안된다.)
- 사이클(cycle) : 특정 노드에서 시작하여 다시 제자리로 돌아오게 되는 경로
- 무방향 그래프 (undirected graph) : 위의 예시 그래프는 엣지의 방향성이 없다.
- 방향 그래프 (directed graph)
TIP
트리는 사이클이 없는 그래프이다.
사이클이 없다는 것은 특정 노드에서 특정 노드로 이동하는 경로가
단 하나만 존재한다는 것을 의미한다.
# 트리
# 이진트리
자식노드 수가 두개 이하인 트리이다.
- 정 이진트리: 자식노드가 0 또는 2개인 이진트리
- 완전 이진트리: 왼쪽부터 모든 레벨이 완전히 채워진 이진트리
- 변질 이진트리: 자식노드가 하나밖에 없는 이진트리
- 포화 이진트리: 모든 노드가 꽉 차있는 이진트리
- 균형 이진트리(중요): 모든노드 왼쪽 하위트리와 오른쪽 하위트리 높이 차이가 1 이하인 트리 (레드-블랙트리)
- 이진탐색트리: 이진트리의 일종이며, 오른쪽 하위트리에는 현재 노드보다 큰 값들의 노드로만 이루어져 있으며, 왼쪽은 현재 노드보다 작은 값들의 노드로만 이루어져 있다.
- 탐색, 삽입, 삭제 모두 O(nlogn), n은 노드 개수
- 선형적으로 노드들이 (5,4,3,2,1...) 삽입되는 경우 최악의 경우에 연산 시간복잡도가 O(n)이 된다. (균형 트리가 되지 않기때문)
- 삽입에 따른 균형도 유지해주는 트리가 레드블랙트리, AVL트리가 있다.
- map 자료구조가 레드블랙트리에 기반하여 만들어졌기에 각종 연산이 모두 O(nlogn)임을 보장받는다.
# 인접행렬
인접행렬은 정점과 간선의 관계를 나타내는 bool타입의 정사각형 행렬이다. 2차원 정방행렬로 표현되며 a[from][to] == 1이면 간선이 있다는 의미를 갖고, 0은 둘 사이에 간선이 존재하지 않음을 나타낸다.
탐색은 행 중심으로 탐색하는 것이 좋다. C++에서 2차원 배열이 행 별로 캐싱되기 때문에 속도가 더 빠르다.
bool a[4][4] = {
{0,1,1,1},
{1,0,1,0},
{1,1,0,0},
{1,0,0,0}
};
인접행렬을 통해 방문노드를 체크하는 로직은 다음과 같다.
#include<bits/stdc++.h>
using namespace std;
const int V = 10;
bool a[V][V], visited[V];
void go(int from){
visited[from] = 1;
cout << from << "\n";
for(int i=0; i < V; i++){
if(visited[i]){
continue;
}
if(a[from][i]){
go(i);
}
}
}
int main(){
a[1][2] = 1;
a[1][3] = 1;
a[3][4] = 1;
a[2][1] = 1;
a[3][1] = 1;
a[4][3] = 1;
for(int i=0; i < V; i++){
for(int j=0; j < V; j++){
// 간선이 있고 방문하지 않은 노드라면 -> from 노드출력
if(a[i][j] && visited[i] == 0){
go(i);
}
}
}
return 0;
}
# 인접 리스트
인접리스트 구현의 경우 c++의 list 타입을 사용해도 되지만 벡터배열로 구현해도 된다.
// 벡터 배열이며, 각 벡터 인덱스가 인접리스트 노드가 된다.
vector<int> adv[V];
list타입을 쓰지 않고 벡터로 구현하는 이유는 **값 인덱싱에 필요한 연산 소요시간이 O(1)**이기 때문이다. 리스트 타입의 경우 삽입 및 삭제가 O(1)이지만 요소 탐색 및 조회에는 반드시 순차탐색을 해야하므로 O(n)이 소요된다.
벡터의 경우 삽입 및 삭제에 O(n)이지만 조회는 인덱싱을 즉시 하면 되므로 O(1)이 소요된다. (마지막 요소 삽입, 삭제는 O(1)임)
인접리스트로 재귀 로직을 기반으로 한 조회는 다음과 같이 구현된다.
#include<bits/stdc++.h>
using namespace std;
const int V = 10;
// 벡터 배열이며, 각 벡터 인덱스가 인접리스트 노드가 된다.
vector<int> adj[V];
int visited[V];
void go(int from){
visited[from] = 1;
cout << from << "\n";
for (int to : adj[from]){
if(to){
continue;
}else{
go(to);
}
}
}
int main(){
adj[1].push_back(2);
adj[2].push_back(1);
adj[1].push_back(3);
adj[3].push_back(1);
adj[3].push_back(4);
adj[4].push_back(3);
for (int i = 0; i < V; i++){
if(adj[i].size() != 0 && visited[i] == 0){
go(i);
}
}
return 0;
}
# 시공간복잡도 비교
인접행렬과 인접리스트의 공간복잡도는 각각 다음과 같다.
O(정점 수^2)O(정점 + 간선 수)
간선이 존재하는지 여부를 조회하는 시간복잡도는 다음과 같다.
O(1): 배열 인덱싱O(V): 연결리스트 형태이므로 순차탐색이 이루어져야함. (최악의 경우 모든 정점이 한 리스트에 연결)
모든 간선들을 조회하는 데에는 다음과 같은 시간복잡도가 필요하다.
O(V^2)O(V+E)
그래프가 널럴하게 연결되어 있는 경우 인접리스트를 사용하며, 빽빽하게 연결되어 있는 경우 인접행렬을 사용한다. 보통은 인접리스트를 사용함
# 지도와 방향벡터
좌표로 표현된 지도 형태의 문제를 풀이한다고 가정해보자.
1 1 1
1 1 1
1 0 0
1로 표기된 구역은 갈 수 있는 구역이며 0은 갈 수 없는 구역일때, 1로 표기된 구역끼리는 간선으로 연결된 그래프라고 볼 수 있다. 하지만 이를 인접리스트나 인접행렬로 변형하여 풀이하면 안된다.
특정 좌표 기준으로 상-하-좌-우 방향으로 조회를 해야하는 문제는 어떻게 풀이해야하나?
int dy[4] = {-1, 0, 1, 0};
int dx[4] = {0, 1, 0, -1};
for(int i=0; i<4; i++){
ny = y + dy[i];
nx = x + dx[i];
}
위와 같이 좌표의 변화율을 담는 배열을 마련하고 방향의 갯수(상하좌우)만큼 for문 순회와 함께 다음 좌표를 설정하게 된다.(ny는 next-y, dy는 direction-y)
dy-dx는 원점을 기준으로 하는 방향벡터가 되는 것이다. visited 등의 데이터 구성은 아래와 같이 하면 된다.
const int V = 3;
int visited[V][V];
int a[V][V];
int dy[4] = {-1, 0, 1, 0};
int dx[4] = {0, 1, 0, -1};
# DFS(Depth First Search)
그래프 탐색 시 사용되는 알고리즘이며 출발 노드로부터 가장 멀리 있는 노드까지 재귀적으로 탐색하는 알고리즘이다. 방문한 정점은 다시 방문하지 않는다.
DFS(u, adj)
u.visited = true
// 노드 U와 연결된 정점 v 순회
for each v in adj[u]
// v를 방문하지 않았었다면
if v.visited == false
// 순회
DFS(v, adj)
#include<bits/stdc++.h>
using namespace std;
const int V = 9;
int visited[V];
vector<int> adj[V];
void dfs(int u){
visited[u] = 1;
cout << u << "순회 중.."
<< "\n";
for(int v : adj[u]){
if(visited[v] == 0){
dfs(v);
}
}
cout << u << "에서 시작된 DFS가 종료되었음"
<< "\n";
return;
}
// 0
// 1 2
// 3 4 8
// 5
int main(){
adj[0].push_back(1);
adj[0].push_back(2);
adj[1].push_back(3);
adj[1].push_back(4);
adj[4].push_back(5);
adj[2].push_back(8);
dfs(0);
return 0;
}
// 스위프트 버전 DFS
import Foundation
var visited: [Int] = .init(repeating: 0, count: 9)
var adj: [[Int]] = .init(repeating: [], count: 10000)
func dfs(_ u: Int) {
visited[u] = 1
print("순회 중..", u)
for v in adj[u] {
if visited[v] == 0 {
dfs(v)
}
}
print("\(u)에서 시작된 DFS 종료")
return
}
adj[0].append(1)
adj[0].append(2)
adj[1].append(3)
adj[1].append(4)
adj[4].append(5)
adj[2].append(8)
dfs(0)
DFS 구현에는 크게 두가지 방법이 있다.
- 방문 전에 다음 노드의
visited여부를 체크하여 순회 여부를 결정하거나, - 일단 다음 노드를 순회하고 나서 현재 노드가
visited라면 리턴하는 방식이다.
// 1번
void dfs(int here){
visited[here] = 1;
for(int there : adj[here]){
if(visited[there] ){
continue;
}
dfs(there);
}
}
// 2번
void dfs(int here){
// 현재 노드가 이미 방문했던 노드라면 리턴
if(visited[here]){
return;
}
visited[here] = 1;
for(int there : adj[here])[
dfs(there);
]
}
# 연결된 컴포넌트
아래는 전체 그래프 내에 연결된 컴포넌트 수를 알아내는 방법이다. DFS를 통해 처리한다.
#include<bits/stdc++.h>
using namespace std;
int dy[4] = {-1, 0, 1, 0};
int dx[4] = {0, 1, 0, -1};
int m,n,k,y,x,ret,ny,nx,t;
int a[104][104];
bool visited[104][104];
void dfs(int y, int x){
visited[y][x] = 1;
for (int i = 0; i < 4; i++){
ny = y + dy[i];
nx = x + dx[i];
if(ny < 0 || ny >= n || nx < 0 || nx >= m){
continue;
}
if(a[ny][nx] == 1 && visited[ny][nx] == 0){
dfs(ny, nx);
}
}
return;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
cin >> a[i][j];
}
}
// DFS순회를 진행하면서 자동으로 visited가 true처리된다.
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
if(a[i][j] == 1 && visited[i][j] == 0){
ret++;
dfs(i, j);
}
}
}
cout << ret << "\n";
return 0;
}
// 스위프트 버전
import Foundation
let dy = [-1, 0, 1, 0], dx = [0, 1, 0, -1]
var visited: [[Bool]] = .init(repeating: [], count: 104)
var adj: [[Int]] = .init(repeating: [], count: 104)
var n = 0, m = 0, y = 0, x = 0, ret = 0, ny = 0, nx = 0
func dfs(_ y: Int, _ x: Int) {
visited[y][x] = true
for i in 0..<4 {
ny = y + dy[i]
nx = x + dx[i]
if ny < 0 || nx < 0 || ny >= n || nx >= m {
continue
}
if adj[ny][nx] == 1 && !visited[ny][nx] {
dfs(ny, nx)
}
}
}
let nm = readLine()!.split(separator: " ").map { Int($0)! }; n = nm[0]; m = nm[1]
for i in 0..<n {
adj[i] = readLine()!.split(separator: " ").map { Int($0)! }
visited[i] = .init(repeating: false, count: m)
}
for i in 0..<n {
for j in 0..<m {
if adj[i][j] == 1 && !visited[i][j] {
dfs(i, j)
ret += 1
}
}
}
print(ret)
//5 5
//1 0 1 0 1
//1 1 0 0 1
//0 0 1 1 1
//0 0 1 1 1
//0 1 0 0 0
//출력결과 4
# BFS
BFS는 레벨별로 노드들을 탐색한다. 큐 자료구조를 기반으로 구현한다.
- 큐에 노드를 푸시한다.
- 큐의 front를 pop한다.
- 그 다음 노드들을 푸시한다.
- 해당 레벨 노드들을 모두 pop하면 그 다음 레벨 노드들을 푸시한다.
슈도코드는 아래와 같다.
// G는 그래프, u는 노드
queue<int> q;
q.push(here);
visited[here] = 1;
while(q.size()){
int here = q.front();
q.pop();
for(int there : adj[here]){
if(visited[there]){
continue;
}
// 방문처리만 하는 문제의 경우에는 +1만 해도 된다.
visited[there] = visited[here] + 1;
q.push(there);
}
}
// 스위프트 버전
var visited: [Int] = .init(repeating: 0, count: 104)
var adj: [[Int]] = .init(repeating: [], count: 104)
let nodeList = [10, 12, 14, 16, 18, 20, 22, 24]
func bfs(_ here: Int) {
var q = Queue<Int>()
visited[here] = 1
q.enqueue(here)
while(!q.isEmpty) {
guard let here = q.front else { return }
_ = q.dequeue()
for there in adj[here] {
if visited[there] == 1 { continue }
visited[there] = visited[here] + 1
q.enqueue(there)
}
}
}
adj[10].append(12)
adj[10].append(14)
adj[10].append(16)
adj[12].append(18)
adj[12].append(20)
adj[20].append(22)
adj[20].append(24)
bfs(10)
print(visited[24])
visited배열을 레벨별로 다른 가중치로 주는 이유는 BFS를 가중치를 둔 최단거리 알고리즘에서도 사용하기 때문이다. (레벨간 가중치는 모두 동일해야한다.) 큐에서 pop이 된 이후에 순회되는 노드들은 레벨이 하나 더해지는것과 동일한 것이다.
BFS예제이다. 출발지 <cury, curx>부터 도착지 <desty, destx>까지의 최단거리를 출력해야한다.
#include<bits/stdc++.h>
using namespace std;
int n, m;
int cury, curx;
int desty, destx;
int ret = 1;
int visited[104][104];
int a[104][104];
int dy[4] = {-1, 0, 1, 0};
int dx[4] = {0, 1, 0, -1};
queue<pair<int, int>> q;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
cin >> cury >> curx;
cin >> desty >> destx;
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
cin >> a[i][j];
}
}
visited[cury][curx] = 1;
q.push({cury, curx});
while (q.size()){
int y, x;
tie(y, x) = q.front();
q.pop();
int ny;
int nx;
for (int i = 0; i < 4; i++){
ny = y + dy[i];
nx = x + dx[i];
if(ny < 0 || nx < 0 || ny >= n || nx >= m){
continue;
}
if(visited[ny][nx] == 0 && a[ny][nx]){
q.push({ny, nx});
visited[ny][nx] = visited[y][x] + 1;
}
}
}
cout << visited[desty][destx] - visited[cury][curx] + 1 << "\n";
return 0;
}
// 5 5
// 0 0
// 4 4
// 1 0 1 0 1
// 1 1 1 0 1
// 0 0 1 1 1
// 0 0 1 1 1
// 0 0 1 1 1
// 답 : 9
// 2차원 BFS 스위프트 버전
func bfs(_ here: (Int, Int)) {
var q = Queue<(Int, Int)>()
visited[here.0][here.1] = 1
q.enqueue(here)
while(!q.isEmpty) {
guard let here = q.dequeue() else { return }
for i in 0..<4 {
let ny = dy[i] + here.0
let nx = dx[i] + here.1
if ny < 0 || nx < 0 || ny >= n || nx >= m || adj[ny][nx] == 0 {
continue
}
if visited[ny][nx] != 0 {
continue
}
visited[ny][nx] = visited[here.0][here.1] + 1
adj[ny][nx] = visited[ny][nx]
q.enqueue((ny, nx))
}
}
}
# 트리 순회
- 후위 순회 - 자식노드 방문을 마치고 자신을 방문
// 인접리스트 기반
vector<int> adj[1004]; // 각 인접리스트는 노드이며, [0]이 left, [1]이 right를 의미한다고 가정한다.
int visited[1004];
void postOrder(int here){
if(visited[here] == 0){
// 트리에 자식노드가 하나
if(adj[here].size() == 1){
postOrder(adj[here][0]);
}
// 트리에 자식노드가 둘 -> 왼-오 순회
if(adj[here].size() == 2){
postOrder(adj[here][0]);
postOrder(adj[here][1]);
}
// 자식노드 순회 마친 뒤 자기자신 순회
visited[here] = 1;
cout << here << " ";
}
}
- 전위순회 - 자기 자신을 먼저 순회한 뒤 자식노드 순회 (코드상으로 후위순회와 재귀함수 호출 위치만 변경된것)
void preOrder(int here){
if(visited[here] == 0){
visited[here] = 1;
cout << visited[here] << "\n";
// 트리에 자식노드가 하나
if(adj[here].size() == 1){
postOrder(adj[here][0]);
}
// 트리에 자식노드가 둘 -> 왼-오 순회
if(adj[here].size() == 2){
postOrder(adj[here][0]);
postOrder(adj[here][1]);
}
}
}
- 중위순회 - 왼쪽노드, 자신노드, 오른쪽노드 순서로 순회한다.
void inOrder(int here){
if(visited[here] == 0){
// 왼쪽 자식노드만 있는경우
if(adj[here].size() == 1){
inOrder(adj[here][0]);
visited[here] = 1;
cout << here << " ";
// 왼쪽 오른쪽 자식노드 둘다 있는경우
}else if(adj[here].size() == 2){
inOrder(adj[here][0]);
// 중간에 자기자신 순회
visited[here] = 1;
cout << here << "\n";
inOrder(adj[here][1]);
// 자식노드 아예 없는경우
}else{
visited[here] = 1;
cout << here << "\n";
}
}
}